New rule:
"X": "F+[[X]-X]-F[-FX]+X"
angle_step set to 25.
axiom is -X.
We don't draw anything for X, it's just a control character we use for the rules.
New rule:
"X": "F+[[X]-X]-F[-FX]+X"
angle_step set to 25.
axiom is -X.
We don't draw anything for X, it's just a control character we use for the rules.

Fractal Plant L-System
An extension to the L-System adding a stack so that we can push, and pop, the current state. This is typically denoted with a [ and ].
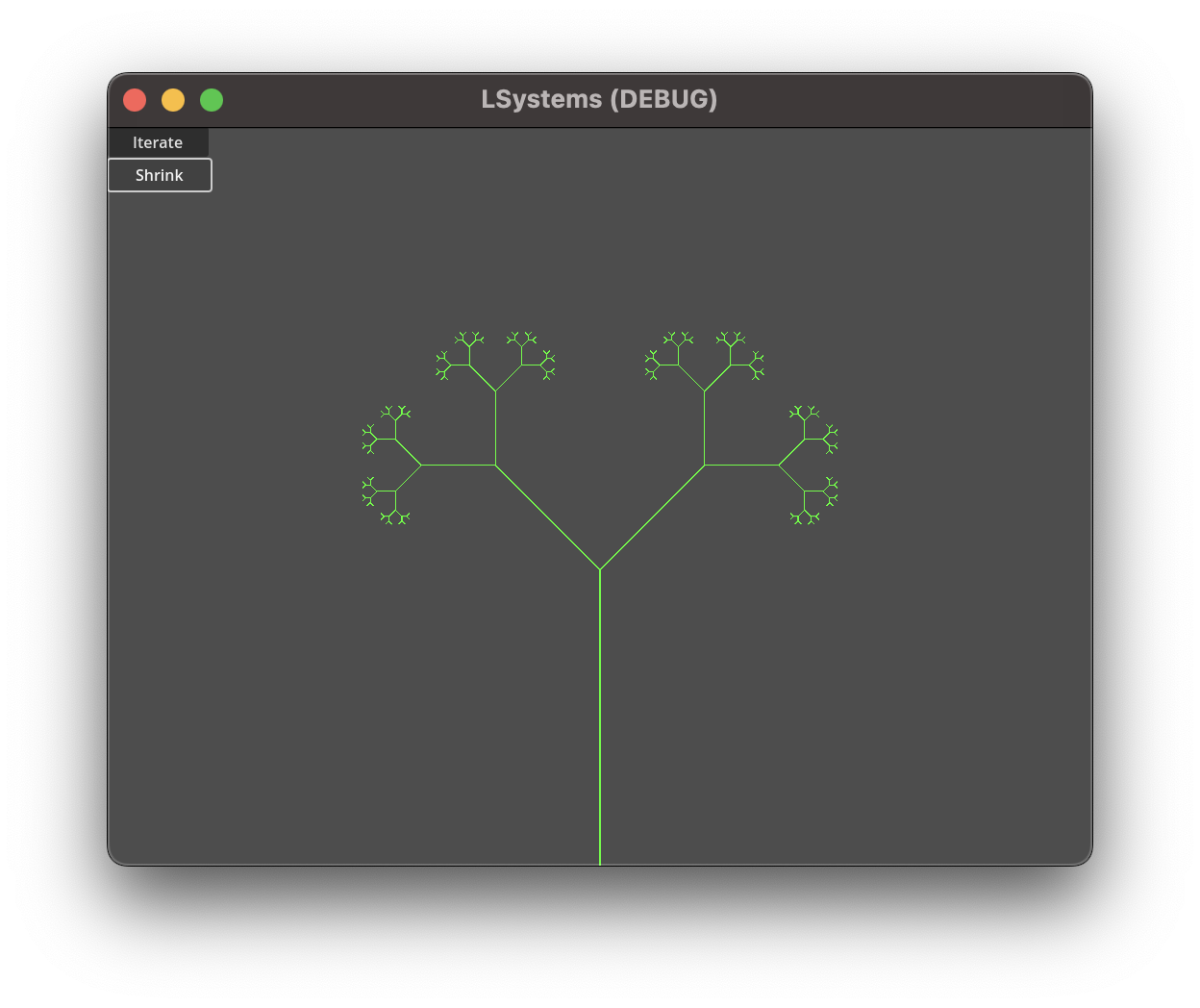
Binary Tree L-System
This is a simple as adding a stack array which we push a copy of the current position and angle into, and pop (copy the last of the stack over our current one and delete it) when we encounter those rules.
However, since we're starting to get a little complicated I decided to create a dictionary of commands so I can sub in alternatives when an L-System calls for slightly different behaviours for the same command.
var commands = {}
func _init():
commands["F"] = func draw_forward_command(current: LNode, stack: Array):
draw_forward(current, stack)
commands["A"] = func draw_forward_command(current: LNode, stack: Array):
draw_forward(current, stack)
commands["B"] = func draw_forward_command(current: LNode, stack: Array):
draw_forward(current, stack)
commands["0"] = func draw_forward_command(current: LNode, stack: Array):
draw_forward(current, stack)
commands["1"] = func draw_forward_command(current: LNode, stack: Array):
draw_forward(current, stack)
commands["+"] = func rotate_left(current: LNode, stack: Array):
current.angle -= angle_step
commands["-"] = func rotate_right(current: LNode, stack: Array):
current.angle += angle_step
commands["["] = func push(current: LNode, stack: Array):
stack.push_back(LNode.new(current.angle, current.position))
current.angle += angle_step
commands["]"] = func pop(current: LNode, stack: Array):
var c = stack[-1]
current.angle = c.angle
current.position = c.position
stack.remove_at(stack.size() - 1)
current.angle -= angle_stepAnd the _draw() function is updated to:
func _draw():
var start_x = (get_window().size.x / 2) * (1 / scale.x)
var start_y = (get_window().size.y) * (1 / scale.y)
var position = Vector2(start_x, start_y)
var angle = 0
var current = LNode.new(angle, position)
var stack = []
for command in axiom:
commands.get(command, ignore).call(current, stack)The axiom is set to 0 and the rules are:
0 → 1[+0]-0
1 → 11
The angle change is set to 45 degrees.
Nothing really changed from the original version... two new rules:
A → B-A-B
B → A+B+A
And our starting axiom is A.
Both A and B mean to draw forward at the current angle, - means to turn left 60 degrees, and + means turn right 60 degrees.
Iterations 1: B-A-B
Iteration 2: A+B+A-B-A-B-A+B+A
...

Sierpinkski triangle L-System
Tweaked the code a little to scale the canvas rather than changing the step length. To ensure it looks good I increase the line width by the inverse of the scale. Due to the way the rules are applied, the triangle is rendered inverted every other iteration. To compensate I use the iteration counter to flip the starting angle to keep it visible.