New rule:
"X": "F+[[X]-X]-F[-FX]+X"
angle_step set to 25.
axiom is -X.
We don't draw anything for X, it's just a control character we use for the rules.
New rule:
"X": "F+[[X]-X]-F[-FX]+X"
angle_step set to 25.
axiom is -X.
We don't draw anything for X, it's just a control character we use for the rules.

Fractal Plant L-System
An extension to the L-System adding a stack so that we can push, and pop, the current state. This is typically denoted with a [ and ].
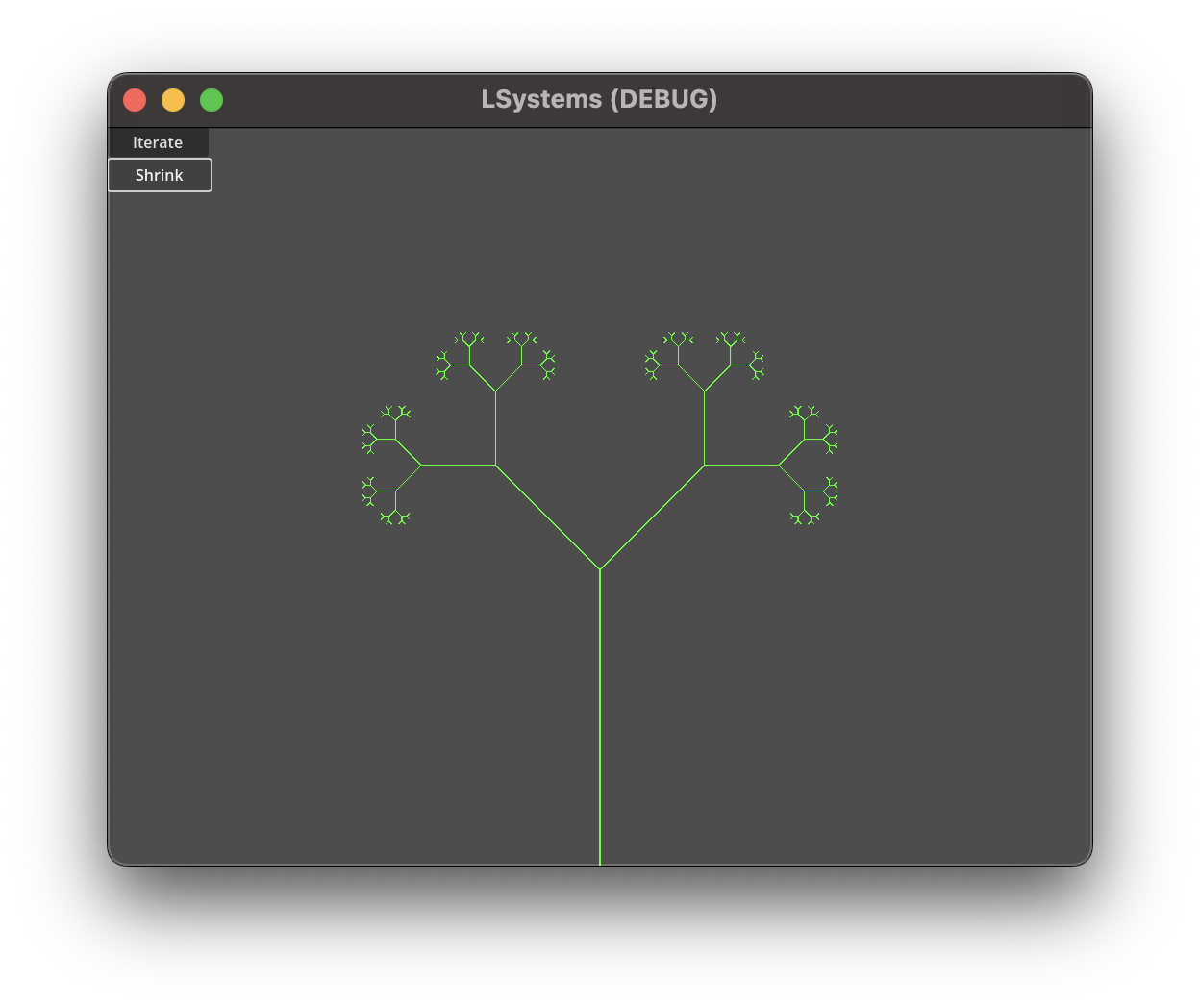
Binary Tree L-System
This is a simple as adding a stack array which we push a copy of the current position and angle into, and pop (copy the last of the stack over our current one and delete it) when we encounter those rules.
However, since we're starting to get a little complicated I decided to create a dictionary of commands so I can sub in alternatives when an L-System calls for slightly different behaviours for the same command.
var commands = {}
func _init():
commands["F"] = func draw_forward_command(current: LNode, stack: Array):
draw_forward(current, stack)
commands["A"] = func draw_forward_command(current: LNode, stack: Array):
draw_forward(current, stack)
commands["B"] = func draw_forward_command(current: LNode, stack: Array):
draw_forward(current, stack)
commands["0"] = func draw_forward_command(current: LNode, stack: Array):
draw_forward(current, stack)
commands["1"] = func draw_forward_command(current: LNode, stack: Array):
draw_forward(current, stack)
commands["+"] = func rotate_left(current: LNode, stack: Array):
current.angle -= angle_step
commands["-"] = func rotate_right(current: LNode, stack: Array):
current.angle += angle_step
commands["["] = func push(current: LNode, stack: Array):
stack.push_back(LNode.new(current.angle, current.position))
current.angle += angle_step
commands["]"] = func pop(current: LNode, stack: Array):
var c = stack[-1]
current.angle = c.angle
current.position = c.position
stack.remove_at(stack.size() - 1)
current.angle -= angle_stepAnd the _draw() function is updated to:
func _draw():
var start_x = (get_window().size.x / 2) * (1 / scale.x)
var start_y = (get_window().size.y) * (1 / scale.y)
var position = Vector2(start_x, start_y)
var angle = 0
var current = LNode.new(angle, position)
var stack = []
for command in axiom:
commands.get(command, ignore).call(current, stack)The axiom is set to 0 and the rules are:
0 → 1[+0]-0
1 → 11
The angle change is set to 45 degrees.
Nothing really changed from the original version... two new rules:
A → B-A-B
B → A+B+A
And our starting axiom is A.
Both A and B mean to draw forward at the current angle, - means to turn left 60 degrees, and + means turn right 60 degrees.
Iterations 1: B-A-B
Iteration 2: A+B+A-B-A-B-A+B+A
...

Sierpinkski triangle L-System
Tweaked the code a little to scale the canvas rather than changing the step length. To ensure it looks good I increase the line width by the inverse of the scale. Due to the way the rules are applied, the triangle is rendered inverted every other iteration. To compensate I use the iteration counter to flip the starting angle to keep it visible.
Playing with Godot 4 and re-visiting L-Systems as a familiarisation exercise.

Koch snowflake on the 3rd iteration
As before, we use a string to track the current state of the iterations and our rules in a dictionary. For each iteration, we loop over the characters in the axiom and, for each character, execute the rule (append the matching value, or the current character, to a new axiom string).
Not shown is the LNode class for holding the angle and the current position. I could track them in the same class I’m using for everything else. However, I know from previous work, I will want to store the state if I continue.
class_name LNode
var angle: float
var position: Vector2
func _init(a: float, p: Vector2):
angle = a
position = p
Fixed a couple of bugs which was keeping the generation from truly finishing which makes increasing the frequency of the branches more feasible. I tweaked the previous generation to increase how often it branched as it approaches the centre. It's still way to messy and chaotic to be a workable solution but for something so basic and naive it actually does better than I expected.
Tweaking values - went a little high on the mountain frequency.
Refining it down. Kind of fun to jump around right until you fall to the bottom ;)
That's more like it!

The 9th iteration of the Sierpinski triangle.
An extension of yesterday's work with L-Systems. The Sierpinski Triangle.
Firstly, I updated the implementation to draw the shape over a number of frames. This is not the end goal of this work so I'm doing it in Unity by drawing to a texture which is easy to implement but far from the most efficient ;) In this case it was best to limit the texture size to 512x512 to avoid a severe performance hit when redrawing the texture. If I needed to, I could simulate a larger texture by mapping it to multiple smaller ones but that's out of scope for the moment.
Next I updated the rules implementation to support multiple rules. Previously I used a single string and a regular expression. This no longer worked because the rules have to be applied simultaneously. Instead, I used a Dictionary to store the rules and, since the rules I need at the moment are only applied to a single character I could simply enumerate the axiom and use the character as the key to the dictionary. If there's a match I append the rule to a new string. If not I append the character.
There is one additional change that is not described in the notation - after each iteration the angle gets flipped so that it goes from 60 to -60, and back again. This is required to keep the triangle facing the same way at each iteration.
A= Step forward
B = Step forward
+ = +60 degrees
- = -60 degrees
A → B-A-B
B → A+B+A
Axiom: A
After 9 iterations the string has gone from 1 to 39,365 characters.
string Iterate(string axiom) { string newAxiom = ""; foreach (char c in axiom) { string ch = c.ToString(); string replace = null; rules.TryGetValue(ch, out replace); if (replace != null) { newAxiom += replace; } else { newAxiom += ch; } } angle = -angle; Debug.Log ("Axiom Length: " + newAxiom.Length); return newAxiom; } void FixedUpdate() { int length = axiom.Length; for (int i = 0; i < 200; i++) { if (index < axiom.Length) { char c = axiom[index]; if (c == 'F' || c == 'A' || c == 'B') { Vector2 newPoint = NewPoint(currentPoint, stepLength, angle); DrawLine (new Line(currentPoint, newPoint), colors[colIndex % 3]); colIndex++; currentPoint = newPoint; } else if (c == '-') { angle -= angleStep; } else if (c == '+') { angle += angleStep; } index++; } } texture2D.Apply(); }

The Koch Snowflake is the one of the first, and simplest, of the fractals.
Starting with an equilateral triangle:
In total, we've added four new lines and increased the total length of the shape by 1/3. Repeat for the remaining lines and we have completed an iteration. Starting again on the new shape we can repeat the same steps for each of the new lines. As can be seen from the above animation, which only iterates 5 times, the complexity rapidly increases.
Technically this is not actually a Koch Snowflake as that is the shape we approach as we iterate. However, we would need to iterate an infinite number of times to generate a true Snowflake.
Iterating on a single line generates a Koch Curve. The Snowflake, starting from a triangle, is made of three curves.
The Koch Curve can be described by a Lindenmayer (L-) System. This is where we create a string and, each iteration, run a set of rules to replace characters in the string with others. Each character defines a drawing rule which we can follow to draw the shape after the iterations have completed.
F = Step Forward
+ = Rotate 60 degrees right
- = Rotate 60 degrees left
Rules
F → F-F++F-F
Starting with: F++F++F++
Our drawing instructions give us our starting triangle. Iterating, we increase the size of the string and generate more rules. Following them generate the animation above.
float stepLength = 256; string rule = "F-F++F-F"; Vector2 start = new Vector2(128, 128); protected override void Draw () { string axiom = "F++F++F++"; for (int i = 0; i < 5; i++) { axiom = Iterate(axiom); } int index = 0; Color[] colors = new Color[3]{Color.black, Color.red, Color.blue}; int length = axiom.Length; Vector2 currentPoint = start; float angle = 0; int colIndex = 0; while(index < axiom.Length) { char c = axiom[index]; if (c == 'F') { Vector2 newPoint = NewPoint(currentPoint, stepLength, angle); DrawLine (new Line(currentPoint, newPoint), colors[colIndex % 3]); colIndex++; currentPoint = newPoint; } else if (c == '-') { angle -= 60; } else if (c == '+') { angle += 60; } index++; } } string Iterate(string axiom) { Regex regex = new Regex("F"); stepLength /= 3; return regex.Replace(axiom, rule); } Vector2 NewPoint(Vector2 point, float step, float angle) { float radAngle = angle * Mathf.Deg2Rad; float x1 = (point.x + (step * Mathf.Cos(radAngle))); float y1 = (point.y + (step * Mathf.Sin(radAngle))); return new Vector2(x1, y1); }
Try modifying the above to generate new shapes. For example, replacing the '+' with '-' symbols in the starting axiom will create the equilateral triangle facing in the other direction and which starts a different pattern which will never exceed the bounds of the initial equilateral triangle.